Set 8 Problem number 8

• Important Note on Notation

• Problem

• Solution

• Generalized Solution

• Explanation in terms of Figure(s); Extension

• Figure(s)

Problem

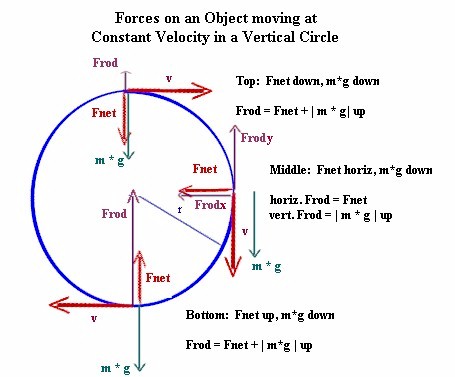
A rigid rod rotating about the center of the circle holds an object in a vertical circle of radius .5099 meters.

• What is the centripetal acceleration of the object?
• If the object has mass 1.759 kg, what is the magnitude of the net force on it?
• If the object moves at a uniform speed of 1 m/s, what is the force exerted by the rod at three points:

• The highest point of its path,
• the lowest point, and
• a point whose altitude is identical to that of the center of the circle.

Solution

The object has uniform speed, so its only acceleration is centripetal:

• | aCent | = v^2 / r = ( 1 m/s)^2 / ( .5099 meters) = 1.961 m/s^2.

The net force at any point is the product of mass and acceleration.  The magnitude of the net force is therefore that of the centripetal force

• | Fcent | = m * | aCent | = m v^2 / r = 1.759 kg * 1.961 m/s^2 = 3.449 Newtons.

Since only the rod and gravity exert forces on the object, at any point the net force on the object is the sum of the forces exerted by the rod and by gravity.

The magnitude of the gravitational force is the weight m * g = 1.759 kg * 9.8 m/s^2 = 17.2382 Newtons

At the top of the arc the net force is toward the center and therefore downward. 

• If we take the upward direction as positive the net force is therefore - 3.449 Newtons, and the weight of the object is - 17.2382 Newtons.
• Since the net force is equal to the sum of the force exerted by the rod and that exerted by gravity we have

• net force = rod force + weight
• rod force = net force - weight = - 3.449 Newtons - (- 17.2382 Newtons) = -3.449 Newtons.

• This tells us that the rod force is upward.   This occurs because the magnitude of the net force is less than the weight: 

• The object doesn't need a centripetal force as great as that of the weight, so to stay in the circular orbit it must avoid experiencing all the force.  
• The rod obliges by supplying an upward force to counter that of the weight. 
• [ Actually this is what the rod has to do in order to avoid being significantly compressed, or even buckled (note that the rod does indeed compress a little; we are implicitly ignoring this tiny deviation in its length and the resulting slight deviation from circular motion). ]

At the bottom of the arc the net force is toward the center and therefore upward. 

• If we take the upward direction as positive the net force is therefore + 3.449 Newtons, and the weight of the object is - 17.2382 Newtons.
• Since the net force is equal to the sum of the force exerted by the rod and that exerted by gravity we have

• net force = rod force + weight
• rod force = net force - weight = 3.449 Newtons - (- 17.2382 Newtons) = 3.448 Newtons.

• This tells us that the rod force is again upward, though this time the rod is being slightly stretched rather than compressed.  This occurs because the net force is in the direction opposite to the weight: 

• The object needs a centripetal force in a direction opposed to its weight, so to keep it in the circular orbit the rod obliges by supplying an upward force in excess of the weight. 
• [ Actually this is what the rod has to do in order to avoid being stretches out of shape or even pulled apart (note that the rod does indeed stretch a little; we are implicitly ignoring this tiny deviation in its length and the resulting slight deviation from circular motion). ]

At the height of the center the net force on the object is toward the center and therefore horizontal, perpendicular to the weight of the object.

• Since there is no other force in the horizontal direction the entire net force must be exerted by the rod, which therefore exerts a force of 3.449 Newtons toward the center of the circle.
• This centripetal force is the net force.  Since it has no component in the vertical direction, the rod must also exert a vertical force equal and opposite to that of the weight.

• We therefore see that the force exerted by the rod has a horizontal component equal to the centripetal force 3.449 Newtons, and a vertical component equal and opposite to the 17.2382 Newton weight.
• The magnitude and direction of this force are easily found in the usual manner using the Pythagorean Theorem and the inverse tangent function.

Generalized Solution

An object of mass m moving on any circle with constant speed has acceleration aCent = v^2 / r.  This is its only acceleration, since it is not changing velocity in the direction of its motion.

• It follows that the object must experience net force Fnet = m * aCent = m v^2 / r.

At any point of its arc is also experiences a downward gravitational force.   If the upward direction is taken as positive we have

• gravitational force = weight = - m * g, where g is the gravitational acceleration g = 9.8 m/s^2.

At any point the net force on the object is therefore the vector sum of its weight and the force exerted by whatever is holding it in its circular path--in this case the rod force:

• net force = centripetal force = gravitational force + rod force.

At the top of the arc centripetal force is downward and we therefore have

• - m v^2 / r = - m * g + rod force, so that
• rod force = m * g - m v^2 / r.

At the bottom of the arc centripetal force is upward so that

• + m v^2 / r = - m * g + rod force, so that
• rod force = m v^2 / r + m * g.

At the altitude of the center of the circle we have

• horizontal net force = centripetal force = m v^2 / r, which must come from the rod since gravity doesn't act in the horizontal direction, and
• vertical net force = vertical rod force + weight = 0 (vertical net force is 0 since the centripetal force has no component in the vertical direction), so that vertical rod force = - weight = + m * g.
• The rod therefore exerts a horizontal force m v^2 / r, either to the right or the left depending on which side of the circle the object is on, and vertical force + m * g.

Explanation in terms of Figure(s); Extension

The figure below shows how at the top of a vertical circle the net force and gravitational forces are both downward, with the net force smaller than the gravitational force, while at the bottom the net force is upward and the gravitational force is downward. 

• As a result the rod must exert a large upward force at the bottom of the circle and a smaller upward force at the top.
• Note that if the net force is greater in magnitude than the gravitational force the rod will have to exert a downward force at the top of the circle.

In the 'middle' of the vertical circle the rod must supply the net force, which is in the horizontal direction, and counter the vertical gravitational force.

Figure(s)