"
Set 8 Problem number 6
What are the centripetal acceleration and
centripetal force holding an object of mass 85.99 kilograms in a circle of radius 5 meters
when the object is moving at 10.99 meters per second?
- The acceleration is v ^ 2 /r = ( 10.99 m/s) ^ 2 / (
5 m) = 24.15 meters per second per second toward the center of the circle.
- To accelerate 85.99 kg at this rate requires F = m * a
= ( 85.99 kg)( 24.15 m/s/s) = 2076 Newtons of force.
- The centripetal acceleration of an object moving
along a circle of radius r at velocity v is a = v^2 / r; this acceleration is directed
toward the center of the circle.
- If the object has mass m, the force required to keep
the object in its circular path is F = m a = m v^2 / r; this force is also directed toward
the center of the circle.
Explanation in terms of Figure(s); Extension
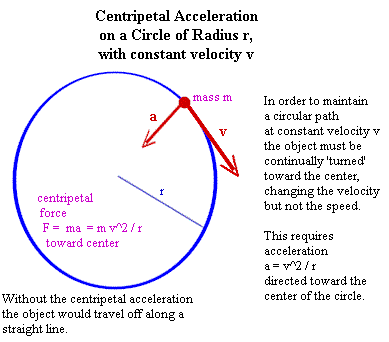
The figure below shows an object moving with
constant speed v on a circle of radius r.
- The acceleration required to keep the object moving
in the circle, as opposed to the straight line along which it would travel if it had no
acceleration, is a = v^2 / r, and is directed toward the center of the circle.
- If the object has mass m, the force required to keep
it on its circular path will therefore be F = m a = m v^2 / r. This force will be directed
in the same direction as the acceleration, toward the center of the circle.
"
