Sane/Demented Problems

To work a problem where the solver has to find the number of demented and sane people at the end of weeks/days/years; he/she could first make a little picture for example:

· See sf #1

·

Then they could use little arrows to show where the percent lost goes (in this case to the demented or sane sides). This way the solver has a picture to look at while they try to work the rest of the problem. Ex.

· See sf #2

·

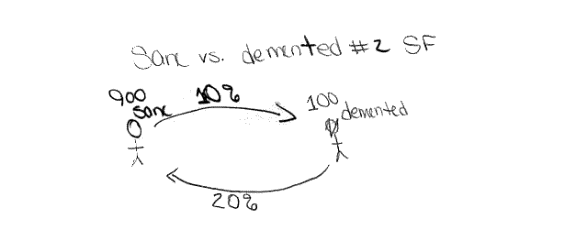
Next the solver takes the number of sane (or demented) people and multiplies that number by the percent it loses. Ex.

· 900 * 0.1=90

This number (90 in the example) is the now subtracted from the number of sane people. Ex.

· 900 - 90= 810

This number (810 in this example) is the number of the sane population that remains sane. Now the solver goes to the demented (or sane) population number and multiplies that number by the percent it loses. Ex.

· 100 * 0.2= 20

Then, as in the first step, you subtract this new number (in this ex. 20) from the population number. Ex.

· 100 – 2= 80

This new number (80) is the number of demented people that stay demented.

Now, since the problem says that the 20% (in this example) that was just subtracted from the demented becomes sane the solver then takes that 20% and adds it to the number of people that remained sane. Ex.

· 810 +80= 890 sane people

The problem also says that 10% of the sane become demented. This 10% is then added to the number of demented people that remained demented. Ex.

· 80 + 90= 170 demented people

Now the solver has the new totals for the sane vs. demented populations and these new totals can be plugged into the above steps to get the numbers of as many transitions as the solver needs. Ex.

· See sf #3