Modeling Population Movement using Matrices

Matrices are useful for modeling population transfer. Here is how to set up a matrix where there are two populations of 500 people each. The first population loses 10% to the second population and gains 20% from the second:

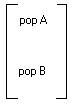
To get the new population for the first group of people, you multiply the first row, first column of the first matrix by the first row, second column of the second matrix, then add the two answers, and the answer goes in the place of pop A. (.9 * 500)+(.2 * 500)= pop A

To get the new population for the second group of people, you multiply the second row, first column of the first matrix by the second row, second column of the second matrix, then add the two answers, and the answer goes in the place of pop B.

(.1 * 500)+(.8 * 500)= pop B.

The decimals in the first matrix show how many people from each population there are. The first row shows that 90% of the first population remains, plus 20% from the second population. The second row shows 10% from the first population plus 80% of the second population’s remaining people.