3)    Now approximate 1/(2^p-1), for your p, to 50 places.  Eliminate the leading zeros and arrange all other digits in ordered pairs in order to plot them.  You can do this in DERIVE.  For the digits 619215665655294138266274489184705902 the syntax would be                                      

[ [6,1],[2,1],[5,6],[6,5],[6,5],[5,2],[9,4],[1,3],[8,2],[6,6],[2,7],[4,4],[8,9],[1,8],[4,7],[0,5],[9,0] ].

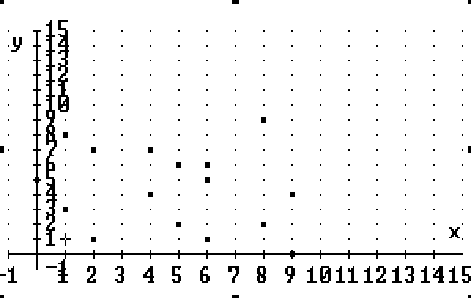
Open a plot window and plot these points, setting an appropriate range.  Does it appear that the digits are indeed random?

After plotting the points, using the example stated in the question, the graph looked like the following:

You must then assess whether they are random or not. Doing this is totally of your own terms. I you so think that these are random then, they are random to you, but another person may see a pattern that you do not. Doing this, then undermines your statement. So in fact this question may or may not have a definite answer.