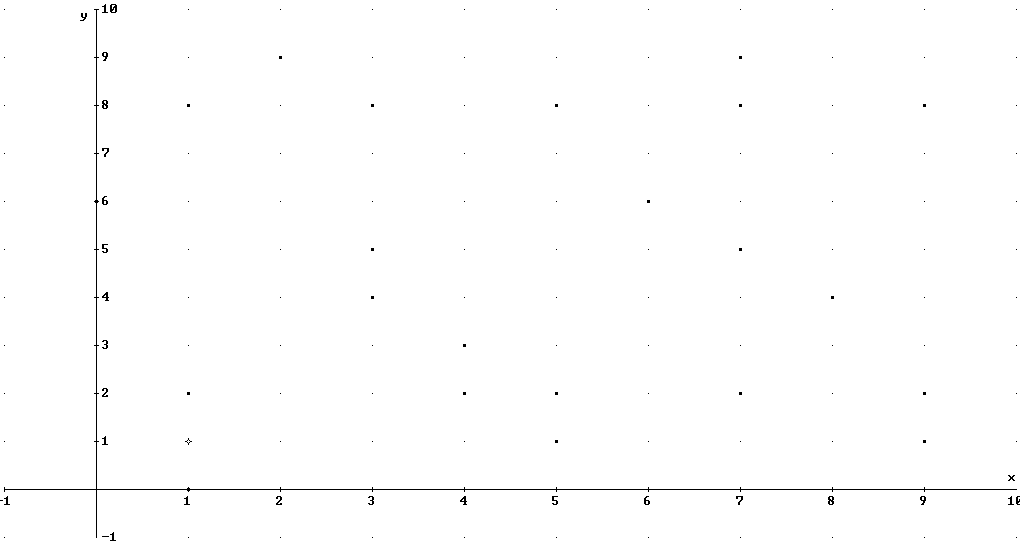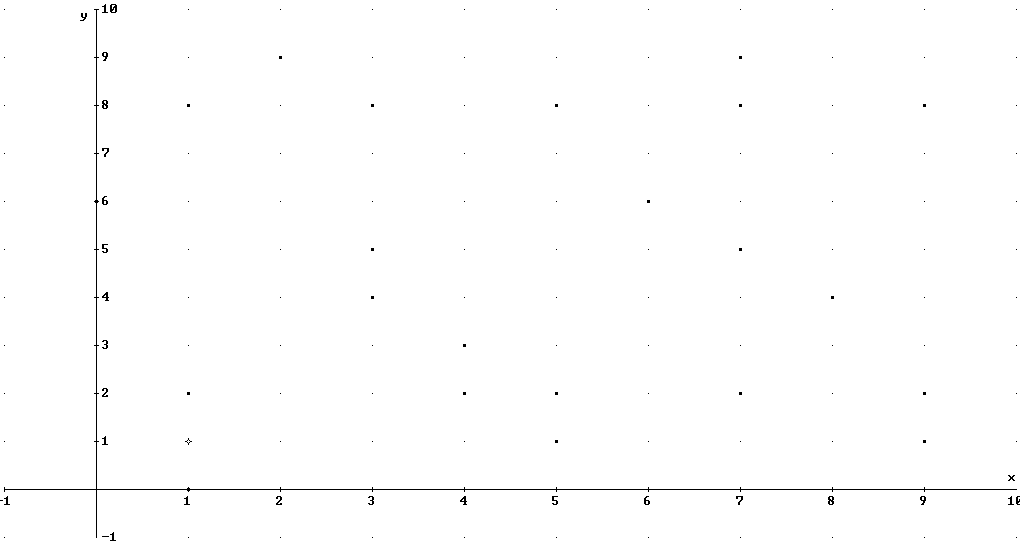
Number 3

First of all this question relates to problem number 2.  If you do not have it completed it will be impossible for you to do this one.  Make sure you are confident of your answer on number 2 before using it in this problem.

Now approximate 1/(2^p-1), for your p, to 50 places.  Eliminate the leading zeros and arrange all other digits into ordered pairs in order to plot them.  You can do this in DERIVE. Open a plot window and plot these points, setting an appropriate range.  Does it appear that the digits are indeed random?

1.  Use the information you got in number two. (2^p-1)

2.  First divide 1 by your answer.

3.  Then, Using derive, approximate that number to 50 places.

4.  Then take those numbers and put them into ordered pairs.

5.  Then open a new plot window as instructed and plot those ordered pairs.

6.  Based on your information, Does the number appear to be random?

- On mine it did, because the points on the graph do not give any specific shape or design or go in any specific line; therefore, I believe that it appears these numbers are random.

p 
2 - 1

p = 50 + 22

p = 72

Prime number closest to 72 is 73

2^73-1

9444732965739290427391

1/(2^p)-1 

1/(2^73)-1
1.0587911840678754238355152297266984379299134121892·10^-22

[[1,0],[5,8],[7,9],[1,1],[8,4],[0,6],[7,8],[7,5],[4,2],[4,2],[3,8],[3,5],[5,1],[5,2],[2,9],

[7,2],[6,6],[9,8],[4,3],[7,9],[2,9],[9,1],[3,4],[1,2],[1,8],[9,2]]

Then just plot these points