Make up population figures for three trees such that the middle tree loses population. Determine how much population is lost, sketch the trapezoidal graph and determine rate of slope change, and explain how this information could have been used to predict the change in population.

(Ex. A) 100 200 100

10 100 180 100 10 Population after first transition.

A tree has a population of 200. The two adjacent trees have a population of 100. There is a uniform 10% transition rate between the trees.

The middle tree would loss population because it is losing more population than it receives from both adjacent trees. (20% of 200= 20*2=40(total loss))

Gain(10% 100= 10*2=20)- loss(40)= total loss or gain(-20)

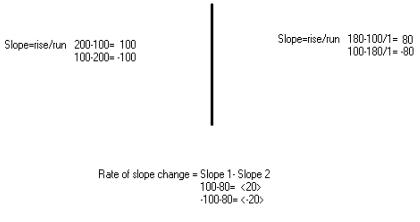
By reading the graph from left to right we realize that from tree 1 there is a slope change of positive 20 therefore tree 1is either gaining population or tree two is losing population, and since tree 2 has a larger initial population it will loss population because the two smaller populated trees to the right and left cannot possibility replenish the trees population to the fullest (Ex. A). From tree 2 to tree three there is a slope change of –20 and the slope is going in a negative direction, so two negatives make a positive slope change, therefore we can determine that either tree 2 is losing population or tree 3 is gaining population. Again tree 2 has a larger base population than the tree to the right and left, and also again tree 2’s population cannot possibly be replenished to the fullest by the two surrounding trees.